Using Parametric Equations to Describe Projectile Motion

The horizontal distance is given by x v0cosθt. Plug this back into your.

Using Parametric Equations To Describe Projectile Motion Study Com

Since v y dy dt it follows that y R gt v 0sinθdt so y 1 2 gt2 v 0sinθtk for some k R.

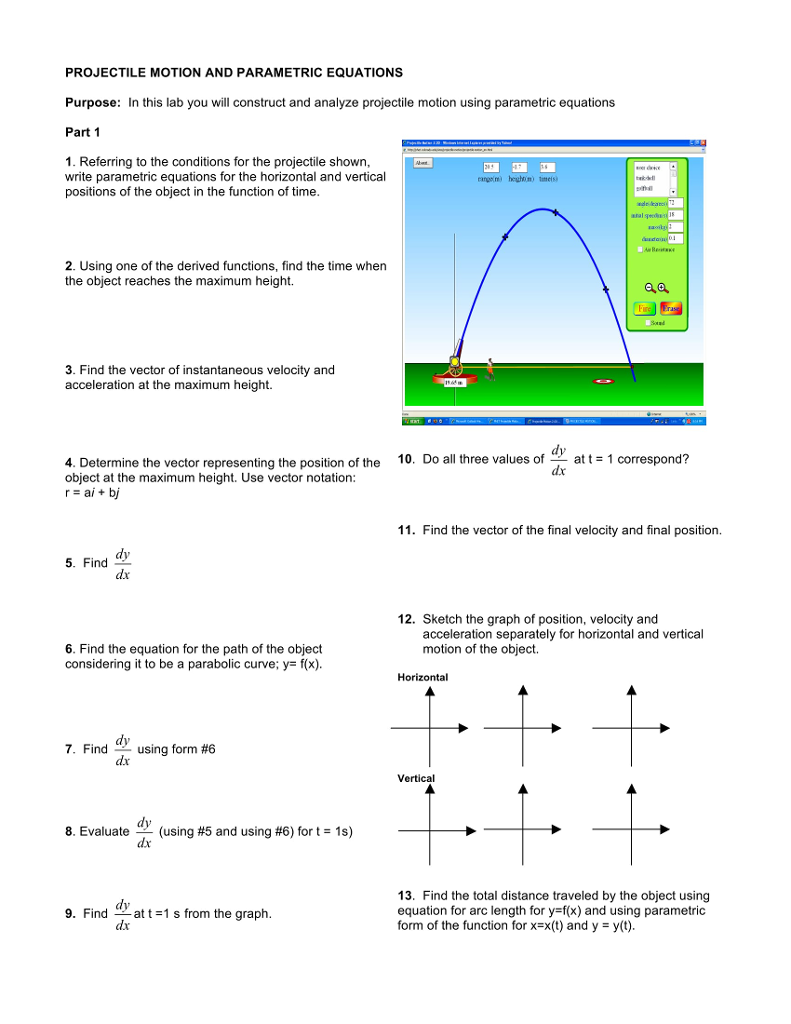
. Parametric equations that describe circular motion will have and as periodic. Ymax 180 What happens to the speed at which the graph is drawn as the ball goes up and back down. Set Tmin 0.

Test an initial velocity and an initial angle and determine if they have chosen the right values to make a basket. Since v y v 0sinθ when t 0 we have v 0sinθ g0c so c v 0sinθ and v y gtv 0sinθ. Bob throws a ball straight up with aninitial speed of 50 feet per second from a height of 6 feeta Find parametric equations that model the motion of theba.

Call the maximum height y h. Identify the conditions that must be met to make a basket. We use information about the initial state of the system as well as the laws of motion to solve for how the object will behave.

2 We now have a set of parametric equations for the motion of the projectile as a function. Y y0 v0 t θ y0 v0 t sinθ - ½ g t2. Equation with respect to t and apply our initial conditions.

Graphing Calculator 40 shows parametric equations in a vector format and Desmos has users put the parameters directly into the coordinate pairs as shown below. H v 0 y 2 2 g. The height of an object affected by gravity is given by the equation h12gtt where g-98 meters per second squared or -32 feet per second squared according to the units of the problem.

Parametric equations can model the path of a projectile. We could introduce an origin as well as a set of and axes on the floor. Paul Kreher Flickr Graphing Parametric Equations by Plotting Points In lieu of a graphing calculator or a computer graphing program plotting points to represent the graph of an equation is the standard method.

Affects the path of a projectile. As a result students will. What is the maximum vertical height achieved by the projectile.

V sindt h Where t is the time and g is the constant acceleration due to gravity approximately 32 fts. The second is projectile motion. Then h v2 0y 2g.

Where V x is the velocity along the x-axis V xo is Initial velocity along the x-axis V y is the velocity along the y-axis V yo is initial velocity along the y-axis g is the acceleration due to gravity t is the time taken. The first is circular motion as was described in the concept problem. Substitute the initial speed of the object for v0.

X v 0 cos θ t. Consider an ant crawling along a flat surface like a floor of a building. The vertical distance is given.

Substitute that angle in degrees for cos θ. Explain how to find velocity speed and acceleration from parametric equations. A traditional use of parametric equations is in physics particulary when we wish to view two dimensional motion as a function of time.

The use of parametric equations to describe motion is what you are tested on during this quiz and worksheet. Use your answer in part7to obtain an expression for the horizontal distance traveled by the projectile. C o s θ.

Model motion in the plane using parametric equations. Questions ask about initial velocity. This equation defines the maximum height of a projectile above its launch position and it depends only on the vertical component of the initial velocity.

1 2 Since y y. Applications of Parametric Equations Parametric Equations are very useful applications including Projectile Motion where objects are traveling on a certain path at a certain time. For example in physics a common scenario is to have a object acted upon by forces.

Explore the motion of a ball thrown directly up theta at a speed of 100 ftsec from a height of 5 ft above the ground. Yt 1 2 gt2 vtsin h. Yrepresent the speed at which the projectile appears to be rising dv y dt g so v y R gdt gtc for some constant c R.

Take your parametric equation for x in part5and solve for t. The standard equations of projectile motion are. Chapter 4 Parametric Equations After completing this unit you will be able to.

Projectile Motion Parametric descriptions of curves occur in many applications. When solving Figure a the expression we found for y is valid for any projectile motion when air resistance is negligible. Y is the vertical position height and x is the horizontal position.

Equations of the path of a projectile fired at an inclination to the horizontal with an initial speed vo from a height h above the horizontal are you will derive these equations in Calc III. Find derivatives and tangent lines for parametric equations. In the x-direction we have x00t 0.

There are two types of parametric equations that are typical in real life situations. The horizontal distance is given by x v 0 cos θ t. 1 The motion in the y-direction is described by y00tg.

Substitute the initial speed of the object for v 0. The expression cos θ cos θ indicates the angle at which the object is propelled. Suppose we want to describe the ants position and the path it takes as it moves.

The vertical position of the projectile after t time is the sum of the distance traveled due to the initial velocity and the distance traveled due to gravity. Substitute that angle in degrees for cosθ. Given a projectile motion problem use parametric equations to solve.

Lets first talk about Simultaneous Solution examples where we might find out whether or not certain objects collide are at the same place at the same time. Sometimes it is written as ½ instead of - ½ but then you need to ensure g is a negative number. The idea of parametric equations.

In particular describe conic sections using parametric equations. Projectile Motion Formula Following are the formula of projectile motion which is also known as trajectory formula. Again assume that the initial point of the projectile is 00.

Discover the parametric equations for the path of a projectile. The expression cosθ c o s θ indicates the angle at which the object is propelled. Consider the following equations for projectile.

X x0 v0 t θ x0 v0 t cosθ. We could approximate the ant as a point and so for each moment in time we could. X v 0 c o s θ t.

1 x vocos8t y -59t.

Lesson 46 Precalculus Projectile Motion With Parametric Equations Youtube

Solved Projectile Motion And Parametric Equations Purpose Chegg Com

Algebra Precalculus Using Parametric Equations To Define The Position Of An Object In Motion Mathematics Stack Exchange